In the previous example we used statements as propositions.  Computer logic is accomplished by using logic gates as building blocks.  A logic gate is a physical circuit which has electrical inputs and usually a single output.

Used in truth tables, we label each input and use truth values to represent weather or not an input is on or off. 

We use the value true , T , 1 to represent on and false , F , 0 to represent off.

Sometimes, On is refered to as a high voltage and off is referred to as a low or no voltage.

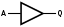
The most common gates are shown in the table below:

Gate		AND	OR	NOT	NAND	NOR	XOR
Symbol
Inputs
A	B	Q=AB	Q=A+B	Q = A	Q= AB	Q=   A+B	Q= A ⊕ B
0	0	0	0	1	1	1	0
0	1	0	1		1	0	1
1	0	0	1	0	1	0	1
1	1	1	1		0	0	0
Description		Outputs 1 when all inputs are 1	Outputs 1 when ANY input is a 1	Inverts the input	Outputs 0 where all inputs are 1	Outputs 1 then both inputs are 0	Outputs 1 when exactly one input is 1
		Outputs 0 otherwise	Outputs 0 otherwise		Outputs 1 otherwise	Outputs 0 otherwise	Outputs 0 otherwise

Typing the mathematical notation into most word processors can be challenging. Sometimes these worded expressions or symbols are used :

Gate	Worded expression	Symbol Expression
AND	A AND B	A^B
OR	A OR B	A v B
NOT	NOT A	~A
NAND	NOT( A AND B)	~(A^B)
NOR	NOT (A OR B)	~(A v B)
XOR	A XOR B	A ∨ B

© 2021  Vedesh Kungebeharry. All rights reserved.